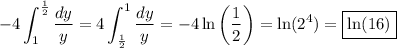We want to evaluate

First we note that the integrand is even (replacing x with -x doesn't fundamentally alter the function being integrated), so this is equal to
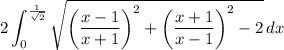
The radicand reduces significantly to
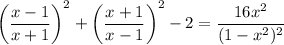
so that taking the square root, we simplify the integral to
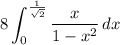
which is trivially computed with a substitution of
 and
and
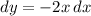 :
: