Answer:
A golfer is teeing off from the middle of a raised tee. The tee is 10.0 meters wide at its base and 3.00 meters above the 25.0 meter wide green, which is sitting on a flat mesa. Assume that the green is circular. The pin (flag) is 120 meters from the base of the tee. He hits his ball with a 7 iron, giving it a velocity of 34.0 m/s at an angle of 40.0 degrees. You must show work for credit. figure attached shows the golf course.
1. The vertical component of velocity = 21.9 m/s
2.The Horizontal component of velocity = 26.1 m/s
3. The time of the flight = 4.6 secs
4. The Maximum height of the golf ball = 27.4 m
5. The golfer reached the green
Step-by-step explanation:
This is a case of projectile motion;
1. The vertical component of velocity
The vertical component of the velocity can be calculated as follows;
 = vsinθ
= vsinθ
 is the vertical velocity
is the vertical velocity
v is the initial velocity = 34 m/s
and θ is the projectile angle =
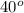
 = (34 m/s) x (sin
= (34 m/s) x (sin
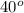 )
)
 = 21.9 m/s
= 21.9 m/s
The vertical velocity is 21.9 m/s
2. The Horizontal component of velocity
The horizontal component of the velocity can be calculated as follows;
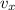 = vcosθ
= vcosθ
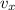 is the horizontal velocity
is the horizontal velocity
v is the initial velocity = 34 m/s
and θ is the projectile angle =
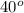
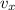 = (34 m/s) x (cos
= (34 m/s) x (cos
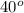 )
)
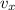 = 26.1 m/s
= 26.1 m/s
The horizontal velocity is 26.1 m/s
3. The time of the flight.
The time of flight can be calculated with the relationship below;
y =
 t -
t -
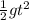
y is the vertical displacement (from the origin) = 0m- 3m = -3 m/s
 is the initial vertical velocity = 21.9 m/s
is the initial vertical velocity = 21.9 m/s
g is the acceleration due to gravity = 9.8 m/

substituting the values in the expression.
3 = (21.9 x t) - (
 x 9.8 x
x 9.8 x
 )
)
3 = 21.9 t - 4.9

rearranging the equation we have;
4.9
 - 21.9 t -3 = 0
- 21.9 t -3 = 0
using the quadratic formula to solve the equation we have;
t = 21.9 ±
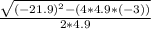
t = −0.133 or 4.6
but time can not be negative so t = 4.6 secs.
The time of flight is 4.6 secs
4. The Maximum height of the golf ball
The maximum height of projectile motion can be obtained thus;
H = h +
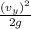
H is the maximum height;
h is the height along the vertical h = 3m;
g is the acceleration due to gravity = 9.8 m/
 .
.
H = 3 +
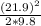
H = 27.4 m
The ball has a height of 27.4 m
5. The distance in reference to the green.
To know the reach, distance covered along the horizontal path and this can be obtained thus;
x =
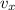 x t
x t
x = 26.1 m/s x 4.6 s
x = 120.06 m
The distance is 120.06 m which is greater than 120 m
Since the distance is more than 120 m the golfer reached the green