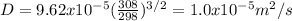Question

An Arnold cell is to be operated as a pseudo-steady-state cell to determine the gas diffusivity of benzene in air at 308 K and 1.0 atm. The 20-cm-long tube, with an inner diameter of 1.0 cm, is initially loaded with liquid benzene to a depth of 1.0 cm from the bottom of the tube. The tube and the liquid are maintained at a constant temperature of 308 K. At this temperature, benzene exerts a vapor pressure of 0.195 atm. Air is continually blown over the top of the tube, removing any of the vaporized benzene vapor; the gas space within the tube is essentially stagnant. At 308 K, liquid benzene’s density is 0:85 g/cm3.

a. It was determined that 72.0 h were required to completely evaporate the benzene initially loaded into the tube. Estimate the binary gas-phase diffusion coefficient for benzene in air using these data.

Answer 1

D=1.0x10^-5 m^2/s

Step-by-step explanation:

the data given by the exercise are as follows:

T=308 K

d=1 cm

PA=0.195 atm

pL=0.85 g/cm^3

The expression for binary gas-phase diffusion coefficient is equal to:

`D=((pL*yB)/(MA((t1^(2)-t2^(2) )/(2) ) )/(c(yA1-yA2)`

`yB=(1-0.805)/(ln((1)/(0.805)) )=0.89`

`C=(P)/(RT)=(1)/(82.06*308)=3.95x10^(-5) mol/cm^(2)`

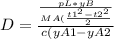
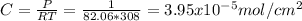
substituting the values ​​in the diffusion equation:

`D=9.6x10^(-6) m^(2)/s`

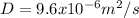
from Appendix J-1 from Welty:

298 K, D=9.62x10^-5 m^2/s

At 308 K, we have the following:

`D=9.62x10^(-5)((308)/(298))^(3/2)=1.0x10^(-5)m^(2)/s`