Question

PPPPLLLLEEEAAASSSEEEE HHHHEEELLLPPP

Big point gain if you answer my question, 35 points thats right 35

f(x)=−4x^2+12x−9

What is the value of the discriminant of fff?

How many xxx-intercepts does the graph of fff have?

Answer 1

d=0 we have one real root (x intercept)

Explanation:

−4x^2+12x−9

The discriminant is

b^2 -4ac

where ax^2 +bx+c

so a = -4 b=12 and c=-9

(12)^2 -4(-4) (-9)

144 -144 =0

The discriminant is 0

If d>0 we have 2 real roots

d =0 we have one real root

d<0 we have no real roots

We have one real root

Answer 2

The value of the discriminant if 0

There is one x-int at (3/2 , 0)

Explanation:

Discriminant equation =
`b^2 - 4ac`

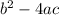
Step 1: Identify a, b, and c

f(x) = −4x^2 + 12x − 9

a b c

So... a = -4, b = 12, c = -9

Step 2: Plug into the formula

`(12)^2-4(-4)(-9)`

`144 - 144`

`0`

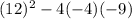
Answer: The value of the discriminant if 0

Step 3: Find the x-intercepts

f(x) = −4x^2 + 12x − 9

f(x) = -(2x - 3)^2

2x - 3 + 3 = 0 + 3

2x / 2 = 3 / 2

x = 3/2

Answer: There is one x-int at (3/2 , 0)