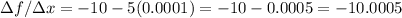Question

Calculate the average rate of change of the given function f over the intervals [a, a + h] where h = 1, 0.1, 0.01, 0.001, and 0.0001. (Technology is recommended for the cases h = 0.01, 0.001, and 0.0001.) HINT [See Example 4.] (Round your answers to five decimal places.) f(x) = 5 x ; a = 1

Answer 1

h=1 df/dx=-15

h=0.1 df/dx=-10.5

h=0.01 df/dx=-10.05

h=0.001 df/dx=-10.005

h=0.0001 df/dx=-10.0005

Explanation:

The function should be 5x^2.

If the function is linear, the answer is very simple: it is 5 for every value of h.

The rate of change can be defined as:

`(\Delta f)/(\Delta x) =(f(a+h)-f(a))/(h)`

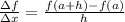
For this function f=5x we have:

`f(a)=5a^2\\\\f(a+h)=5(a+h)^2=5a^2+10ah+5h^2`

Then, we have:

`(\Delta f)/(\Delta x) =(f(a+h)-f(a))/(h)=(5a^2-(5a^2+10ah+5h^2))/(h)=-10a+5h`

The value for a is a=1

For h=1

`\Delta f/\Delta x=-10a-5h=-10-5=-15`

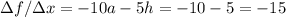
For h=0.1

`\Delta f/\Delta x=-10-5(0.1)=-10-0.5=-10.5`

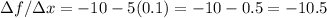
For h=0.01

`\Delta f/\Delta x=-10-5(0.01)=-10-0.05=-10.05`

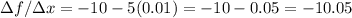
For h=0.001

`\Delta f/\Delta x=-10-5(0.001)=-10-0.005=-10.005`

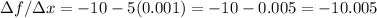
For h=0.0001

`\Delta f/\Delta x=-10-5(0.0001)=-10-0.0005=-10.0005`