Question

Find the size of each of two samples (assume that they are of equal size) needed to estimate the difference between the proportions of boys and girls under 10 years old who are afraid of spiders. Assume the "worst case" scenario for the value of both sample proportions. We want a 98% confidence level and for the error to be smaller than 0.04.

Answer 1

To estimate the difference between the proportions of boys and girls under 10 years old who are afraid of spiders with a 98% confidence level and error less than 0.04, we need at least 849 individuals in each sample using the worst-case scenario of population proportions.

Step-by-step explanation:

To determine the size of each of two samples needed to estimate the difference between the proportions of boys and girls under 10 years old who are afraid of spiders, we need to consider the confidence level and the margin of error we desire. Since we are given a 98% confidence level and an error margin less than 0.04, we will use the worst-case scenario for the population proportions, which is 0.5 (50%), because the variance (p(1-p)) is maximized at this point.

The formula for sample size in this scenario is:

`n = (Z^2 * p * (1-p)) / E^2`

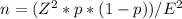
Where:

n is the sample size

Z is the Z-score corresponding to the desired confidence level

p is the estimated population proportion

E is the desired margin of error

The Z-score for a 98% confidence level is approximately 2.33. Using p = 0.5 and E = 0.04, we can calculate the sample size needed.

`n = (2.33^2 * 0.5 * (1-0.5)) / 0.04^2`

`n = (5.4289 * 0.25) / 0.0016`

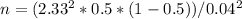
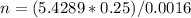
n = 1.357225 / 0.0016

n = 848.265625

Since we need a whole number of individuals, we would round up, so we need at least 849 individuals in each sample to meet the criteria for our study.