Question

A 0.26 kg mass is attached to a light spring with a force constant of 35.9 N/m and set into oscillation on a horizontal frictionless surface. If the spring is stretched 5.0 cm and released from rest, determine the following.

(a) maximum speed of the oscillating mass(b) speed of the oscillating mass when the spring is compressed 1.5 cm

Answer 1

(a) maximum speed of the oscillating mass is 0.588 m/s

(b) speed of the oscillating mass when the spring is compressed 1.5 cm is 0.56 m/s

Step-by-step explanation:

Given;

mass of the object, m = 0.26 kg

force constant, k = 35.9 N/m

spring displacement, A = 5.0 cm

Part (a) maximum speed of the oscillating mass

Vmax. = ωA

Where;

ω is angular speed

A is the maximum displacement

`\omega= \sqrt{(k)/(m)} = \sqrt{(35.9)/(0.26)} = 11.75 \ rad/s`

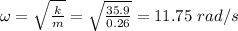
Vmax. = 11.75 x 0.05 = 0.588 m/s

Part (b) speed of the oscillating mass when the spring is compressed 1.5 cm

x = 1.5 cm

`V = \sqrt{(k)/(m)(A^2-x^2) }\\\\ V = \sqrt{(35.9)/(0.26)(0.05^2-0.015^2) } = 0.56 \ m/s`

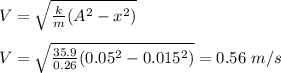
V = 0.56 m/s