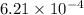Answer:
The fraction of particles is
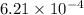
Step-by-step explanation:
Given :
Alpha particle atomic no.
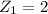
Gold foil atomic number
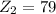
Thickness
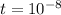 m
m
Density
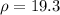
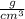
Kinetic energy of alpha particle
 V
V
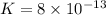 V
V
Scattered angle
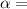 4.5°
4.5°
Fraction of incident particle scattered at angle
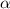 is,
is,
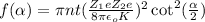
Where
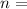 number density of particle,
number density of particle,
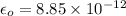
For calculating value of
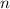
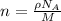
Where
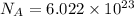 ,
,
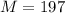 ( Mass number of gold foil )
( Mass number of gold foil )
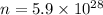
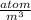
Put the all value in above equation,
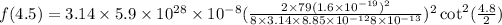
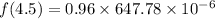
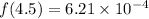
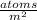
Therefore, the fraction of particles is