Question

A line parallel to a triangle's side splits AB into lengths of x - 6 and x. The other side, AC, is split into lengths of x + 6 and x + 20. What is the length of AC? A) 36 B) 46 C) 56 D) 66

Answer 1

Option C: 56 is the length of AC

Step-by-step explanation:

Let DE be the line parallel to BC

Let D divides the side AB and E divides the side E

The lengths of the sides are
`AD=x-6` ,
`DB=x`,
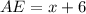`AE=x+6` and
`EC=x+20`

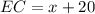
We need to determine the length of AC

The value of x:

By side splitter theorem, we have,

`(AD)/(DB)=(AE)/(EC)`

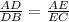
Substituting the values, we have,

`(x+6)/(x)=(x+6)/(x+20)`

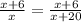
Simplifying, we get,

`(x+6)(x+20)=x(x+6)`

`x^2+20x-6x-120=x^2+6x`

`x^2+14x-120=x^2+6x`

`14x-120=6x`

`8x=120`

`x=15`

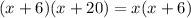
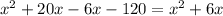
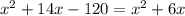
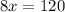
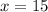
Thus, the value of x is 15

Length of AC:

The length of AC is given by

`AC=AE+EC`

`AC=x+6+x+20`

`AC=15+6+15+20`

`AC=56`

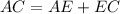
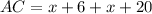
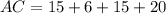
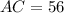
Thus, the length of AC is 56

Hence, Option C is the correct answer.