This an incomplete question, the image of figure is shown below.
Answer : The area of the sector not shaded is, 120π
Step-by-step explanation :
Given:
The angle of the sector = 60°
Radius of the circle = 12 unit
First we have to calculate the area of circle.
Formula used :
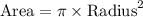
Now put all the given values in this formula, we get:
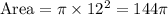
Now we have to calculate the area of sector that are shaded.
Formula used :

Now put all the given values in this formula, we get:
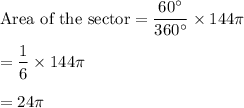
Now we have to calculate the area of sector that is not shaded.
Area of the sector not shaded = 144π - 24π = 120π
Therefore, the area of the sector not shaded is, 120π