Question: (in proper order)
Suppose that you are holding a pencil balanced on its point. If you release the pencil and it begins to fall, what will be the angular acceleration when it has an angle of 10.0 degrees from the vertical?
Part C
What is the distance
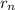 between the point of application of
between the point of application of
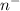 and the axis of rotation? What is the distance
and the axis of rotation? What is the distance
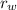 between the point of application of
between the point of application of
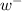 and the axis? Enter your answers in meters separated by a comma.
and the axis? Enter your answers in meters separated by a comma.
Answer:
-17rads/s², 0.075m
Step-by-step explanation:
Here, counterclockwise torques is positive end hence torque due to weight about the pivot point is negative as it is clockwise.
The expression of toque, acting on pencil is given as:
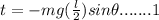
Also, the expression of torque in terms of angular acceleration is given as:
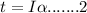
The moment of inertia of the pencil about one end is given as:
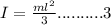
the equation
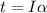 now becomes
now becomes
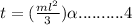
Equating 1 and 4 as expression of torque

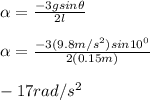
The normal force acting at the normal force only and hence the distance between them is zero.
The effect of gravity begins at half-length of the pencil. Therefore, the distance between the weight and the point of application is 0.075m