Question

Geologists estimate the time since the most recent cooling of a mineral by counting the number of uranium fission tracks on the surface of the mineral. A certain mineral specimen is of such an age that there should be an average of 6 tracks per cm2 of surface area. Assume that the number of tracks in an area follows a Poisson distribution. Let X represent the number of tracks counted in 1 cm2 of surface area.

Compute P(X = 7). Round your answer to four decimal places.

Answer 1

0.1377 is the required probability.

Explanation:

We are given the following information in the question:

The number of tracks in an area follow a Poisson distribution.

Mean number of track per area = 6 tracks per
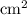`\text{cm}^2` of surface area.

`\lambda = 6`

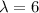
Formula:

`P(x =k) = \displaystyle(\lambda^k e^(-\lambda))/(k!)\\\\ \lambda \text{ is the mean of the distribution}`

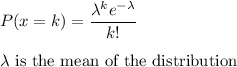
We have to evaluate

P(x = 7)

`P(x = 7)= \displaystyle(\lambda^7 e^(-\lambda))/(7!) = \displaystyle((6)^7 e^(-6))/(7!)\\\\P(x = 7) = 0.1377`

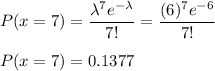
0.1377 is the required probability.