Question

After a fall, a 90 kg rock climber finds himself dangling from the end of a rope that had been 16 m long and 7.8 mm in diameter but has stretched by 3.1 cm. For the rope, calculate

(a) the strain,
(b) the stress, and
(c) the Young's modulus.

Answer 1

Step-by-step explanation:

Given that,

Mass of the rock climber, m = 90 kg

Original length of the rock, L = 16 m

Diameter of the rope, d = 7.8 mm

Stretched length of the rope,
`\Delta L=3.1\ cm`

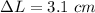
(a) The change in length per unit original length is called strain. So,

`\text{strain}=(\Delta L)/(L)\\\\\text{strain}=(3.1* 10^(-2))/(16)\\\\\text{strain}=0.00193`

(b) The force acting per unit area is called stress.

`\text{stress}=(mg)/(A)\\\\\text{stress}=(90* 10)/(\pi (3.9* 10^(-3))^2)\\\\\text{stress}=1.88* 10^7\ Pa`

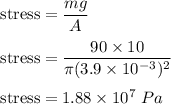
(c) The ratio of stress to the strain is called Young's modulus. So,

`Y=\frac{\text{stress}}{\text{strain}}\\\\Y=(1.88* 10^7)/(0.00193)\\\\Y=9.74* 10^9\ N/m^2`

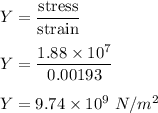
Hence, this is the required solution.