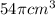Answer : The correct option is, (A)
Step-by-step explanation :
First we have to calculate the volume of cylinder.
Formula used:
Volume of cylinder =
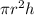
where,
r = radius = 3 cm
h = height = 18 cm (We are assuming that 3 solid spheres stacked to each other = 3 × diameter of each sphere = 3 × 2 × 3 = 18)
Volume of cylinder =
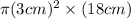
Volume of cylinder =
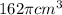
Now we have to calculate the volume of 3 solid spheres.
Formula used:
Volume of 3 spheres =
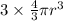
Volume of 3 spheres =
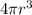
Volume of 3 spheres =

Volume of 3 spheres =
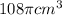
Now we have to calculate the amount of empty space within a cylinder.
Amount of empty space within a cylinder = Volume of cylinder - Volume of 3 spheres
Amount of empty space within a cylinder =
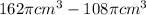
Amount of empty space within a cylinder =
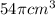
Therefore, the amount of empty space within a cylinder is,