Question 5: prove that it’s =0

Question

asked Jun 7, 2021 69.0k views

1 Answer

Misticos · Answer 1 · 2021-06-12T02:17:31+0000

Answer:

Proof in explanation.

Explanation:

I'm going to attempt this by squeeze theorem.

We know that
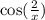$\cos((2)/(x))$ is a variable number between -1 and 1 (inclusive).

This means that
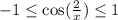$-1 \le \cos((2)/(x)) \le 1$ .

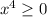$x^4 \ge 0$ for all value
. So if we multiply all sides of our inequality by this, it will not effect the direction of the inequalities.

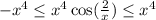
$-x^4 \le x^4 \cos((2)/(x)) \le x^4$

By squeeze theorem, if
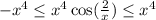
$-x^4 \le x^4 \cos((2)/(x)) \le x^4$

and
$\lim_(x \rightarrow 0)-x^4=\lim_(x \rightarrow 0)x^4=L$ , then we can also conclude that
$\im_(x \rightarrow) x^4\cos((2)/(x))=L$ .

So we can actually evaluate the "if" limits pretty easily since both are continuous and exist at
x=0 .

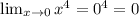
$\lim_(x \rightarrow 0)x^4=0^4=0$

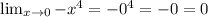$\lim_(x \rightarrow 0)-x^4=-0^4=-0=0$ .

We can finally conclude that
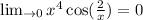$\lim_(\rightarrow 0)x^4\cos((2)/(x))=0$ by squeeze theorem.

Some people call this sandwich theorem.