Question

When purchasing bulk orders of​ batteries, a toy manufacturer uses this acceptance sampling​ plan: Randomly select and test 48 batteries and determine whether each is within specifications. The entire shipment is accepted if at most 2 batteries do not meet specifications. A shipment contains 3000 ​batteries, and 1​% of them do not meet specifications.

a. What is the probability that this whole shipment will be​ accepted?

b. Will almost all such shipments be​ accepted, or will many be​ rejected?

Answer 1

a) the probability that this whole shipment will be​ accepted is 0.8731

b) Almost all shipments (87.31% of the shipments) would be accepted

Explanation:

a) Given that:

p = 1% = 0.01

n = 48

Binomial probability states that

`P(X=x) = (n!)/(x!(n-x)!) .p^(x)(1-p)^(n-x)`

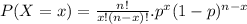
Addition rule for mutually exclusive events is:

P(A or B) = P(A) + P(B)

To get the probability that this whole shipment will be​ accepted we evaluate at x = 0, 1, 2

`P(X=0) = (48!)/(0!(48-0)!) .0.01^(0)(1-0.01)^(48-0)=0.6173\\P(X=1) = (48!)/(1!(48-1)!) .0.01^(1)(1-0.01)^(48-1)=0.1848\\P(X=2) = (48!)/(2!(48-2)!) .0.01^(2)(1-0.01)^(48-2)=0.071`

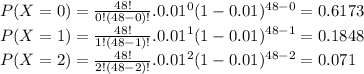
Using addition rule:

P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.6173 + 0.1848 + 0.071 = 0.8731

the probability that this whole shipment will be​ accepted is 0.8731

b) Almost all shipments (87.31% of the shipments) would be accepted