Question

Which is cheaper: eating out or dining in? the mean cost of a flank steak, broccoli, and rice bought at the grocery store is $13.04 (money.msn website, november 7, 2012). a sample of 100 neighborhood restaurants showed a mean price of $12.75 and a standard deviation of $2 for a comparable restaurant meal?

Answer 1

`H_o: \mu \geq 13.04\\H_(\alpha): \mu \geq 13.04`

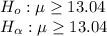
b) 0.0751

c) We cannot afirm whether eating out or dinning in is cheaper

d) do not reject neither.

Questions:

(a). Develop appropriate hypotheses for a test to determine whether the sample data support the conclusion that the mean cost of a restaurant meal is less than fixing a comparable meal at home.

(b). Using the sample from the 100 restaurants, what is the p -value?

(c). At α = .05 ,what is your conclusion?

(d). Repeat the preceding hypothesis test using the critical value approach

Step-by-step explanation:

(b)

`(X-\mu)/(\sigma √(n) ) = P_v\\(12.75-13.04)/(2 √(100) ) = -1.45`

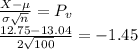
We use excel function to get the Pz which is .0751

(c). 0.0751 > .05 , We cannot reject the hypotesis. Thus, we can neither say dinning in is more cheap nor eating out is cheaper.

(d). With = 99 , t .05 = −1.66 Reject H 0 if ? ≤ −1.66 −1.45 > −1.66 , do not reject

Degrees of freedom = n − 1 = 99 and Pz of 0.05 = -1.66

Reject when Pz < of -1.66

-1.45 > 1.66 threfore we cannot reject the hypotesis.