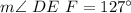Question

If m angle DEF = (6x+37) and mFGD = (19x-31), find m angle DEF

Answer 1

Answer: 127

Explanation:

Answer 2

`m \angle \ DE\ F = 127\°`

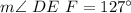
Explanation:

Given:

`m \angle \ DE\ F = (6x+37)`

`m \ arc \ FGD = (19-31)`

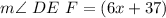
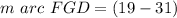
We need to find the m ∠ DEF.

Solution:

Now we can say that;

By inscribed angle theorem;

"The measure of the angle is twice the measure on the arc subtended by it."

so we get;

`2 \ m \angle DE\ F = m\ arc \ FGD`

`2(6x+37)= 19x-31`

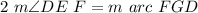
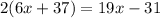
Applying distributive property we get;

`12x+74=19x-31`

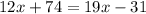
Combining the like terms we get;

`19x-12x=74+31\\\\7x = 105`

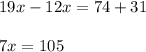
Dividing both side by 7 we get;

`(7x)/(7)=(105)/(7)\\\\x=15`

`m \angle \ DE\ F = (6x+37) = (6* 15+37) = 90+37 =127\°`

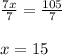
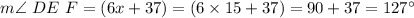
Hence
`m \angle \ DE\ F = 127\°`