Given that the two functions are
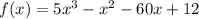 and
and
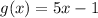
We need to determine the value of

The value of
 :
:
To determine the value of
 , let us substitute the functions
, let us substitute the functions
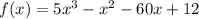 and
and
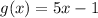 in
in

Thus, we get;
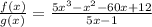
Let us group the terms in the numerator.
Thus, we get;
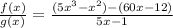
Factoring out the common terms from each group, we get;
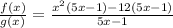
Factoring out the term (5x - 1), we have;
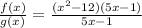
Cancelling the common terms, we get;
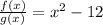
Thus, the value of
 is
is
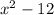
Hence, Option A is the correct answer.