Question

If you pour whisky over ice, the ice will cool the drink, but it will also dilute it. A solution is to use whisky stones. Suppose Ernest pours 55.0 g of whisky at 22 ∘C room temperature, and then adds three whisky stones to cool it. Each stone is a 32.0 g soapstone cube that is stored in the freezer at -11 ∘C. The specific heat of soapstone is 980 J/kg⋅K; the specific heat of whisky is 3400 J/kg⋅K.What is the final temperature of the whisky?

Answer 1

To find the final temperature of the whisky after adding whisky stones, we need to calculate the heat transfer between the whisky and the stones. We can use the specific heat and temperature changes of the stones and whisky to determine the final temperature of the whisky.

Step-by-step explanation:

To calculate the final temperature of the whisky after adding the whisky stones, we need to consider the heat transfer between the whisky and the stones. First, we need to calculate the heat absorbed by the stones using the formula Q = mcΔT, where Q is the heat absorbed, m is the mass, c is the specific heat, and ΔT is the temperature change. For the stones, the mass is 32.0 g, the specific heat is 980 J/kg⋅K, and the temperature change is the final temperature of the whisky minus -11 ∘C. After calculating the heat absorbed by the stones, we can use the formula Q = mcΔT again to calculate the final temperature of the whisky. This time, the mass is 55.0 g (mass of whisky), the specific heat is 3400 J/kg⋅K, and the temperature change is the final temperature of the whisky minus 22 ∘C. Solving these equations will give us the final temperature of the whisky.

Answer 2

10.1 °C

Step-by-step explanation:

After the mixture, heat is gained by the soapstone cubes (they were at a lower temperature) while heat is lost by the whisky (it was at a higher temperature).

Let the temperature of the mixture be T.

Heat lost by whisky,
`H_W = m_Wc_W\Delta\theta_W`

`m_W` is the mass of the whisky (in kg),
`c_W` is the specific heat of whisky (J/kg·K) and
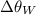`\Delta\theta_W` is the change in temperature of the whisky (in °C or K).

`H_W = (0.055\text{ kg})(3040\text{ J/kg}\cdot\text{K})(22-T) = 167.2(22-T) \text{ J}`

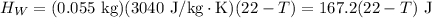
Heat gained by soapstone cubes,
`H_C = m_Cc_C\Delta\theta_C`

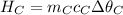
There are three cubes of soapstone, so their mass is multiplied by 3.

`H_W = (3*0.032\text{ kg})(980\text{ J/kg}\cdot\text{K})(T-(-11)) = 94.08(T+11) \text{ J}`

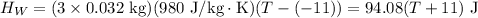
From the principle of mixtures,

Heat lost by whisky = Heat gained by soapstone cubes (assuming no heat loss to the surroundings)

`167.2(22-T) = 94.08(T+11)`

`3678.4 - 167.2T = 94.08T + 1034.88`

`2643.52 = 261.28T`

`T= 10.1`

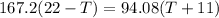
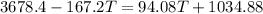
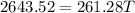
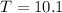
The final temperature of the whisky is 10.1 °C.