Question

Find the interior angle on a regular polygon with 40 sides...

please explain

Answer 1

Given that the regular polygon with 40 sides.

We need to determine the interior angle of the polygon.

Sum of the interior angle:

Sum of the interior angle can be determined using the formula,

`(n-2)* 180^(\circ)`

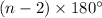
where n is the number of side.

Substituting
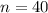`n=40` in the above formula, we get;

`(40-2)*180^(\circ)`

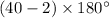
Simplifying the values, we get;

`38*180^(\circ)=6840^(\circ)`

Thus, the sum of the interior angles is 6840°

Measure of each interior angle:

The measure of each interior angle can be determined using the formula,

`((n-2)* 180^(\circ))/(n)`

where n is the number of side.

Substituting
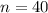`n=40` in the above formula, we get;

`((40-2)* 180^(\circ))/(40)`

Simplifying the values, we get;

`(38* 180^(\circ))/(40)=(6480)/(40)`

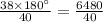
Dividing, we get,

`n=171^(\circ)`

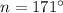
Thus, the measure of each interior angle is 171°