Question

In 1901, Thomas Edison invented the nickel-iron battery. The follwing reaction takes place in the battery.

Fe(s) + 2 NiO(OH)(s) + 2 H2O(l) Fe(OH)2(s) + 2 Ni(OH)2(aq)

How many mole of Fe(OH)2, is produced when 3.60 mol Fe and 8.20 mol NiO(OH) react?

Answer 1

Answer: The number of moles of
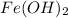`Fe(OH)_2` produced are, 3.60 moles.

Explanation :

First we have to calculate the limiting and excess reagent.

The balanced chemical equation is:

`Fe(s)+2NiO(OH)(s)+2H_2O(l)\rightarrow Fe(OH)_2(s)+2Ni(OH)_2(aq)`

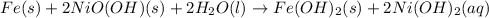
From the balanced reaction we conclude that

As, 1 mole of
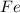`Fe` react with 2 mole of
`NiO(OH)`

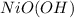
So, 3.60 moles of
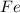`Fe` react with
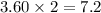`3.60* 2=7.2` moles of
`NiO(OH)`

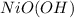
From this we conclude that,
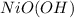`NiO(OH)` is an excess reagent because the given moles are greater than the required moles and
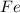`Fe` is a limiting reagent and it limits the formation of product.

Now we have to calculate the moles of
`Fe(OH)_2`

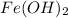
From the reaction, we conclude that

As, 1 mole of
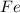`Fe` react to give 1 mole of
`Fe(OH)_2`

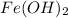
So, 3.60 mole of
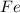`Fe` react to give 3.60 mole of
`Fe(OH)_2`

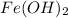
Therefore, the number of moles of
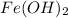`Fe(OH)_2` produced are, 3.60 moles.