Question

Which inequalities would have an open circle when graphed? Check all that apply.

Answer 1

It is given that the inequalities.

We need to determine the inequalities which have an open circle.

The graph will have an open circle only if it has the symbol < or > because it indicates that the boundary is not included.

Option A:
`t \geq 25`

The inequality shows that it contains the boundary point 25.

Hence, the inequality
`t \geq 25` does not have an open circle.

Hence, Option A is not the correct answer.

Option B:
`-2.5 \leq m`

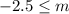
The inequality shows that it contains the boundary point -2.5.

Hence, the inequality
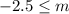`-2.5 \leq m` does not have an open circle.

Hence, Option B is not the correct answer.

Option C:
`x>5.4`

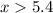
The inequality shows that it does not contains the boundary point 5.4

Hence, the inequality
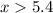`x>5.4` have an open circle.

Thus, Option C is the correct answer.

Option D:
`(1)/(2)>x`

The inequality shows that it does not contain the boundary point
`(1)/(2)`

Hence, the inequality
`(1)/(2)>x` have an open circle.

Thus, Option D is the correct answer.

Option E:
`x>0`

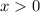
The inequality shows that it does not contain the boundary point 0

Hence, the inequality
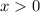`x>0` have an open circle.

Thus, Option E is the correct answer.