a)
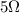 , 1.6 A
, 1.6 A
b)
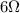 , 1.33 A
, 1.33 A
Step-by-step explanation:
a)
In this situation, we have two resistors connected in series.
The equivalent resistance of resistors in series is equal to the sum of the individual resistances, so in this circuit:
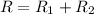
where
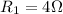
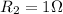
Therefore, the equivalent resistance is
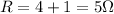
Now we can use Ohm's Law to find the current flowing through the circuit:
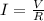
where
V = 8 V is the voltage supplied by the battery
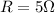 is the equivalent resistance of the circuit
is the equivalent resistance of the circuit
Substituting,
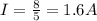
The two resistors are connected in series, therefore the current flowing through each resistor is the same, 1.6 A.
b)
In this part, a third resistor is added in series to the circuit; so the new equivalent resistance of the circuit is
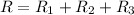
where:
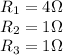
Substituting, we find the equivalent resistance:
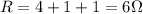
Now we can find the current through the circuit by using again Ohm's Law:
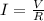
where
V = 8 V is the voltage supplied by the battery
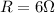 is the equivalent resistance
is the equivalent resistance
Substituting,
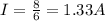
And the three resistors are connected in series, therefore the current flowing through each resistor is the same, 1.33 A.