the additive inverse of non complex 9 is -9 .
Explanation:
Complex number is said to be the sum of whole numbers and imaginary numbers.The additive inverse of the any number is the changing the sign of the number. That is instead –ve sign is positive and vice versa.
Additive Inverse of Complex Numbers:
Let take the complex numbers
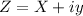 and its inverse be
and its inverse be
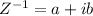
Step 1: Now add the Z and Z-1, we get

Step 2: Combine Like term, we get

Step 3: By using zero product property, we can equating as
 and
and
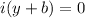
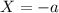 and
and
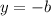
Thus, the additive inverse of the complex numbers
 .
.
Now, additive inverse of
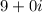 =
=
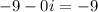 .
.
Therefore , the additive inverse of non complex 9 is -9 .