Answer:
The values of a, b and c are:
Explanation:
Step 1:
First Confirm the sequence is quadratic by finding the second difference.
Sequence =
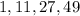
1st difference:
2nd difference:
Step 2:
Just divide the second difference by 2, you will get the value of
 .
.
6 ÷ 2 = 3
So the first term of the nth term is
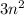
Step 3: Next, substitute the number 1 to 5 into
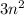
n = 1,2,3,4,5
3n² = 3,12,27,48,75
Step 4:
Now, take these values (3n²) from the numbers in the original number sequence and work out the nth term of these numbers that form a linear sequence.
n = 1,2,3,4,5
3n² = 3,12,27,48,75
Differences:
1 - 3 = -2
11 - 12 = -1
27 - 27 = 0
49 - 48 = 1
Now the nth term of these differences (-2,-1,0,1) is (n - 1) - 2.
so b = 1, and c = -3
Step 5: Write down your final answer in the form an² + bn + c.
3n² + (n - 1) -2
= 3n² + n - 1 - 2
= 3n² + n - 3
Therefore, the values of a, b and c are: