Question

The nth term of this sequence is ansquared+by+c
1,11,27,49
Find the values of a b and c

Answer 1

The values of a, b and c are:

• a = 3

• b = 1

• c = -3

Explanation:

Step 1:

First Confirm the sequence is quadratic by finding the second difference.

Sequence =
`1,11,27,49`

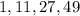
1st difference:

• 11-1=10

• 27-11=16

• 49-27=22

2nd difference:

• 16-10=6

• 22-16=6

Step 2:

Just divide the second difference by 2, you will get the value of
`a`.

6 ÷ 2 = 3

So the first term of the nth term is
`3n^(2)`

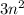
Step 3: Next, substitute the number 1 to 5 into
`3n^(2)`

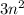
n = 1,2,3,4,5

3n² = 3,12,27,48,75

Step 4:

Now, take these values (3n²) from the numbers in the original number sequence and work out the nth term of these numbers that form a linear sequence.

n = 1,2,3,4,5

3n² = 3,12,27,48,75

Differences:

1 - 3 = -2

11 - 12 = -1

27 - 27 = 0

49 - 48 = 1

Now the nth term of these differences (-2,-1,0,1) is (n - 1) - 2.

so b = 1, and c = -3

Step 5: Write down your final answer in the form an² + bn + c.

3n² + (n - 1) -2

= 3n² + n - 1 - 2

= 3n² + n - 3

Therefore, the values of a, b and c are:

• a = 3

• b = 1

• c = -3