Domain questions are basically validity checks. Since you cannot have a negative number in a square root without creating an imaginary number, that takes out the bottom two.
A quick tip: substitute the value for x. If the equation is valid (no imaginary numbers, not dividing by 0, etc, that function has the given domain.
ex:

Negative square roots lead to imaginary numbers so this is not the domain for this problem. The Domain for this one is
 since that is the lowest possible value of x you can have that is valid.
since that is the lowest possible value of x you can have that is valid.
To answer your question, since I assume you are pressed for time,
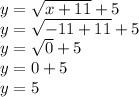
so the first one is the function that has the given domain.