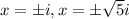Question

What are the solutions of the equation x4 + 6x2 + 5 = 0? Use u substitution to solve.

x = i and x = i 5

X=+ i and x i 5

x=+ -1 and x= + -5

x= -1 and x= + - 5

Answer 1

The solutions of the equation are
`x=\pm i, x=\pm √(5)i`

Step-by-step explanation:

Given that the equation is
`x^(4)+6 x^(2)+5=0`

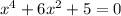
We need to determine the solutions of the equation.

Let us substitute
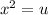`x^(2) =u` and
`x^4=u^2`

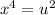
Thus, the equation becomes,

`u^(2)+6 u+5=0`

Factoring the equation, we get;

`(u+1)(u+5)=0`

`u=-1, u=-5`

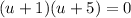
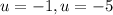
Substituting back
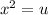`x^(2) =u` and solve for x.

First, we shall substitute
`u=-1`

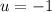
Thus, we get;

`x^(2) =-1`

`x=√(-1)`

`x=\pm i`

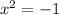
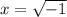
Similarly, substituting
`u=-5`, we get;

`x^(2) =-5`

`x=√(-5)`

`x=\pm √(5)i`

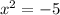
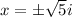
Thus, the solutions of the equation are
`x=\pm i, x=\pm √(5)i`