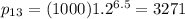Question

A culture started with 1, 000 bacteria . After 2 hours , it grew to 1, 20 bacteria . Predict how many bacteria will be present after 13 hours . Round your answer to the nearest whole number.

Answer 1

3271

Explanation:

In this problem, we have:

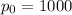`p_0 = 1000` is the population of bacteria at the beginning, at time t = 0

After 2 hours, we have a number of bacteria equal to

`p(2)=1200`

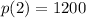
This means that the growth of the population for every 2 hours is:

`(p(2))/(p_0)=(1200)/(1000)=1.2`

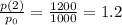
This means that we can write an expression for the population after n pairs of hours as follows:

`p(n)=p_0 1.2^n`

where

n is the number of "pairs of hours" passed from t = 0

In this problem, we want to find the population of bacteria after 13 hours, which contains a number of pairs of hours equal to:

`n=(13)/(2)=6.5`

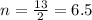
Therefore, substituting 6.5 in the expression, we find the population after 13 hours:

`p_(13)=(1000)1.2^(6.5)=3271`