Answer:
Probability that the mean of a sample of 90 computers would be less than 117.13 months is 0.0033.
Explanation:
We are given that the quality control manager at a computer manufacturing company believes that the mean life of a computer is 120 months, with a standard deviation of 10 months.
Also, a random sample of 90 computers is selected.
Firstly, Let
 = mean of a sample of 90 computers
= mean of a sample of 90 computers
The z score probability distribution for is given by;
Z =
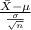 ~ N(0,1)
~ N(0,1)
where,
 = mean life of a computer = 120 months
= mean life of a computer = 120 months
 = standard deviation = 10 months
= standard deviation = 10 months
n = sample of computers = 90
Probability that the mean of a sample of 90 computers would be less than 117.13 months is given by = P(
 < 117.13 months)
< 117.13 months)
P(
 < 117.13) = P(
< 117.13) = P(
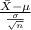 <
<
 ) = P(Z < -2.72) = 1 - P(Z
) = P(Z < -2.72) = 1 - P(Z
 2.72)
2.72)
= 1 - 0.99674 = 0.0033
Therefore, probability that the mean of a sample of 90 computers would be less than 117.13 months is 0.0033.