Question

A spaceprobe in outer space is flying with a constant speed of 1.530 km/s. The probe has a payload of 1363.0 kg and it carries 3486.0 kg of rocket fuel. The rocket engines of the probe are capable of expelling propellant at a speed of 3.795 km/s. Then the rocket engines are fired up. How fast will the spaceprobe travel when all the rocket fuel is used up

Answer 1

6.33 km/s

Step-by-step explanation:

Given that :

A spaceprobe in outer space is flying with a constant speed
`v_i` = 1.530 km/s.

The probe has a payload = 1363.0 kg

which carries 3486.0 kg of rocket fuel.

Exhaust speed = 3.795 km/s

How fast will the spaceprobe travel when all the rocket fuel is used up?

As we know that the rate of change of spaceprobe momentum is equal to the thrust of the rocket.

Then;

`m (dv)/(dt) = -v_(ex) (dm)/(dt)`

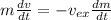
where;

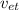`v_{et` = exhaust speed

`dv = -v_(ex)(dm)/(m)`

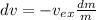
Taking the integral of the above expression; we have:

`v_f -v_i = - v_(ex)In m|^(m_f)_(m_o)`

`v_f -v_i = - v_(ex)In (m_o)/(m_f)`

`v_f = v_i + v_(ex)In (m_o)/(m_f)`

`v_f =1.530 + 3.795 In ((1363+3486)/(1363) )`

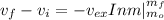
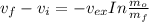
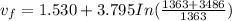
= 6.33 km/s