Question

A researcher believes that 8% of pet dogs in Europe are Labradors. If the researcher is right, what is the probability that the proportion of Labradors in a sample of 644 pet dogs would be greater than 6%? Round your answer to four decimal places.

Answer 1

Proportion of Labradors in a sample of 644 pet dogs would be greater than 6% is 0.9838.

Explanation:

We are given that a researcher believes that 8% of pet dogs in Europe are Labradors.

We have to find the probability that the proportion of Labradors in a sample of 644 pet dogs would be greater than 6%.

Let p = % of pet dogs in Europe that are Labradors = 8%

The z score probability distribution is given by;

Z =
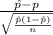`\frac{\hat p -p}{\sqrt{(\hat p(1- \hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of Labradors

n = sample of pet dogs = 644

So, probability that the proportion of Labradors in a sample of 644 pet dogs would be greater than 6% is given by = P(
`\hat p` > 6%)

P(
`\hat p` > 6%) = P(
`\frac{\hat p -p}{\sqrt{(\hat p(1- \hat p))/(n) } }` >
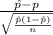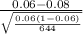`\frac{0.06 -0.08}{\sqrt{(0.06(1- 0.06))/(644) } }` ) = P(Z > -2.14)

= P(Z < 2.14) = 0.9838 {using z table directly}

Hence, the probability that the proportion of Labradors in a sample of 644 pet dogs would be greater than 6% is 0.9838.