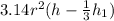Answer:
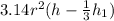
Explanation:
Let h be the cylinders height and r the radius.
-The volume of a cylinder is calculated as:
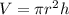
-Since the cone is within the cylinder, it has the same radius as the cylinder.
-Let
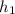 be the height of the cone.
be the height of the cone.
-The area of a cone is calculated as;
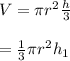
The volume of the solid section of the cylinder is calculated by subtracting the cone's volume from the cylinders:
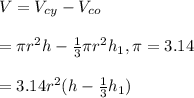
Hence, the approximate area of the solid portion is