Answer:
The value of test statistics is 1.06.
Explanation:
We are given that according to a marketing research study, American teenagers watched 14.8 hours of social media posts per month last year, on average. A random sample of 11 American teenagers was surveyed and the mean amount of time per month each teenager watched social media posts was 15.6. This data has a sample standard deviation of 2.5.
We have to test if the mean amount of time American teenagers watch social media posts per month is greater than the mean amount of time last year or not.
Let, NULL HYPOTHESIS,
 :
:
 = 14.8 hours {means that the mean amount of time American teenagers watch social media posts per month is same as the mean amount of time last year}
= 14.8 hours {means that the mean amount of time American teenagers watch social media posts per month is same as the mean amount of time last year}
ALTERNATE HYPOTHESIS,
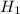 :
:
 > 14.8 hours {means that the mean amount of time American teenagers watch social media posts per month is greater than the mean amount of time last year}
> 14.8 hours {means that the mean amount of time American teenagers watch social media posts per month is greater than the mean amount of time last year}
The test statistics that will be used here is One-sample t-test;
T.S. =
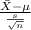 ~
~
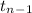
where,
 = sample mean amount of time per month each teenager watched social media posts = 15.6 hours
= sample mean amount of time per month each teenager watched social media posts = 15.6 hours
 = sample standard deviation = 2.5 hours
= sample standard deviation = 2.5 hours
n = sample of teenagers = 11
So, test statistics =
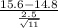 ~
~
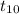
= 1.06
Hence, the value of test statistics is 1.06.