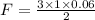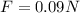Answer:
0.09 N
Step-by-step explanation:
We are given that
Radius of disk,r=6 cm=
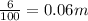
1 m=100 cm
B=1 T
Current,I=3 A
We have to find the frictional force at the rim between the stationary electrical contact and the rotating rim.
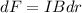
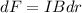
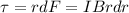
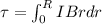

Torque due to friction

Where friction force=F
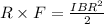

Substitute the values