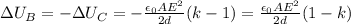a)
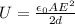
b)
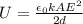
c)
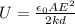
d)
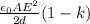
Step-by-step explanation:
a)
The electric potential energy stored in a capacitor is given by:
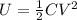 (1)
(1)
where
C is the capacitance
V is the potential difference across the capacitor
For a parallel-plate capacitor, the capacitance is
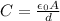
where
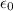 is the vacuum permittivity
is the vacuum permittivity
A is the area of the plates
d is the separation between the plates
Moreover in this problem, the potential difference across the capacitor is equal to the EMF of the battery:
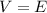
Substituting the last two expressions into eq.(1), we find the potential energy in the capacitor:
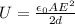
b)
In this second part, a polymer slab with thickness d (the same as the separation between the plates) and relative permittivity k is inserted into the capacitor.
When a dielectric is inserted into a capacitor, its capacitance increases due to the polarization effect on the molecules of the dielectric, according to the equation

where
C' is the new capacitance
k is the relative permittivity
C is the original capacitance
In this case, the dielectric is inserted while the battery is still connected: this means that the potential difference across the capacitor remains the same, only the capacitance changes.
If we look at eq.(1), we see that the potential energy is directly proportional to the capacitance of the capacitor. Therefore, since the capacitance has increased by a factor k, the potential energy will also increase by a factor k, therefore:
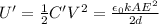
c)
In this case, the dielectric is removed, the battery disconnected, and the dielectric is inserted again keeping the battery disconnected.
This means that the potential difference V does not remain the same across the capacitor: however, the charge stored remains the same (since the capacitor is disconnected from everything, it cannot discharge).
The initial charge stored in the capacitor is
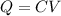
where
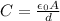 is the initial capacitance
is the initial capacitance
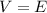 is the initial potential difference
is the initial potential difference
So
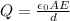
The charge remains constant, while the capacitance changes when the dielectric is inserted, and it becomes
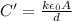
where k is the relative permittivity.
To find the new energy stored in the capacitor, we use the other formula:
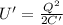
which is equivalent to eq.(1). Substituting everything, we find:
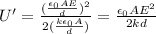
d)
Here we want to find the change in the potential energy of the battery during the process described in part b).
Due to the law of conservation of energy, the total energy of the battery + the capacitor must be constant. This means that
 (2)
(2)
where
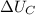 is the change in potential energy of the capacitor
is the change in potential energy of the capacitor
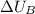 is the change in potential energy of the battery
is the change in potential energy of the battery
From part a) and b), we can find the change in potential energy of the capacitor:

And so according to eq.(2), the change in the potential energy of the battery is