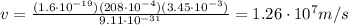Question

A beam of electrons moving in the x-direction enters a region where a uniform 208-G magnetic field points in the y-direction. The boundary of the field region is perpendicular to the beam.If the beam penetrates 3.45 mm into the field region, what's the electrons' speed

Answer 1

`1.26\cdot 10^7 m/s`

Step-by-step explanation:

When a charged particle moves perpendicularly to a magnetic field, the force it experiences is:

`F=qvB`

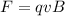
where

q is the charge

v is its velocity

B is the strength of the magnetic field

Moreover, the force acts in a direction perpendicular to the motion of the charge, so it acts as a centripetal force; therefore we can write:

`qvB=m(v^2)/(r)`

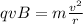
where

m is the mass of the particle

r is the radius of the orbit of the particle

The equation can be re-arranges as

`v=(qBr)/(m)`

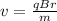
where in this problem we have:

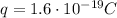`q=1.6\cdot 10^(-19)C` is the magnitude of the charge of the electron

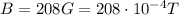`B=208 G=208\cdot 10^(-4)T` is the strength of the magnetic field

The beam penetrates 3.45 mm into the field region: therefore, this is the radius of the orbit,

`r=3.45 mm = 3.45\cdot 10^(-3) m`

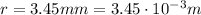
`m=9.11\cdot 10^(-31) kg` is the mass of the electron

So, the electron's speed is

`v=((1.6\cdot 10^(-19))(208\cdot 10^(-4))(3.45\cdot 10^(-3)))/(9.11\cdot 10^(-31))=1.26\cdot 10^7 m/s`