Answer:
Mass of HD 68988 is ≅ 1.2 times the mass of sun.
Step-by-step explanation:
Given :
Orbital distance
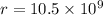 m
m
Time period
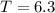 days
days
Now we have to convert time period in seconds
 sec
sec
From the kepler's third law,
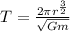
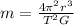
Where

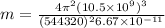
 ≅
≅
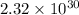 Kg
Kg
Now we have to calculate mass of HD 68988 in terms of sun mass,
Mass of sun =
 Kg
Kg
Therefore mass of HD 68988 is
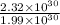 ≅ 1.2 times the mass of sun.
≅ 1.2 times the mass of sun.