Answer:
P ≈ 25 units
Explanation:
LM = 12 units ( horizontal line )
use the distance formula to find length of other 2 sides.
d =
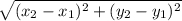
with (x₁, y₁ ) = L (- 3, 2) and (x₂, y₂ ) = M (3, 5 )
LM =
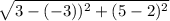
=
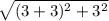
=
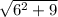
=
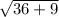
=
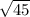
Repeat with (x₁, y₁ ) = M (3, 5) and (x₂, y₂ ) = N (9, 2)
MN =
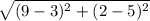
=
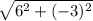
=
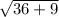
=
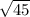
Then perimeter P is the sum of the 3 sides
P = 12 +
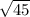 +
+
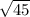 = 12 + 2
= 12 + 2
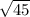 ≈ 25 units ( to the nearest unit )
≈ 25 units ( to the nearest unit )