Question

Let X be the time it takes for a person to choose a birthday gift, where X has an average value of 27 minutes. If the random variable X is known to be exponentially distributed, what are the parameters of this exponential distribution

Answer 1

The parameters of this exponential distribution is
`\lambda` =
`(1)/(27)` .

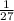Explanation:

We are given that the random variable X is known to be exponentially distributed and let X be the time it takes for a person to choose a birthday gift, where X has an average value of 27 minutes.

So, X = time it takes for a person to choose a birthday gift

The probability distribution function of exponential distribution is given by;

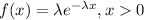`f(x) = \lambda e^(-\lambda x) , x >0` where,
`\lambda` = parameter of distribution.

Now, the mean of exponential distribution is =
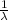`(1)/(\lambda)` which is given to us as average value of 27 minutes that means
`\lambda = (1)/(27)` .

So, X ~ Exp(
`\lambda = (1)/(27)` ) .

Therefore, the parameter of this exponential distribution is
`\lambda` .