Answer:
a) Focus is (1,0)
b) Length of Latus rectum is 4
c) The endpoints of the latus rectum is (1,-2) and (1,2)
Explanation:
The given parabola has equation
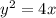
When we compare to
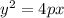
We have
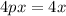
This implies,
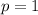
The focus of this parabola is at (p,0).
Therefore the focus is (1,0)
b) The length of the latus rectum is given by
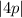
From a) part we found p to be 1.
Substitute p=1 to obtain:
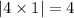
c) The focus is the midpoint of the latus rectum.
Since the focus is (1,0), we substitute x=1 into the equation to see intersection of the latus rectum and the parabola.
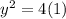
This means that:
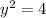
Take square root:
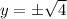
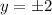
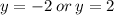
Therefore the end of latus rectum are at (1,-2) and (1,2)