Question

Find coordinates of the focus, the length of the latus rectum, and the coordinates of its endpoint for y^2= 4x

Answer 1

a) Focus is (1,0)

b) Length of Latus rectum is 4

c) The endpoints of the latus rectum is (1,-2) and (1,2)

Explanation:

The given parabola has equation

`{y}^(2) = 4x`

When we compare to

`{y}^(2) = 4px`

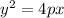
We have

`4px = 4x`

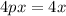
This implies,

`p = 1`

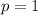
The focus of this parabola is at (p,0).

Therefore the focus is (1,0)

b) The length of the latus rectum is given by

`|4p|`

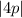
From a) part we found p to be 1.

Substitute p=1 to obtain:

`|4 * 1| = 4`

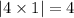
c) The focus is the midpoint of the latus rectum.

Since the focus is (1,0), we substitute x=1 into the equation to see intersection of the latus rectum and the parabola.

`{y}^(2) = 4(1)`

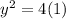
This means that:

`{y}^(2) = 4`

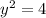
Take square root:

`y = \pm √(4)`

`y = \pm2`

`y = - 2 \: or \: y = 2`

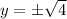
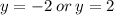
Therefore the end of latus rectum are at (1,-2) and (1,2)