Question

PLEASE HELP!!
what is the derivative of ln(lnx^3)

Answer 1

`f'(x)=(1)/(xln(x))`

Explanation:

In order to solve this problem, we rewrite the original function as:

`f(x)=ln(3 ln(x))`

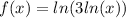
In order to find the derivative, we apply the chain rule for a composite function, which states that:

`(d)/(dx)g(f(x))=(dg)/(df)\cdot (df)/(dx)`

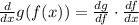
By applying the chain rule, we obtain the following:

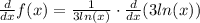`(d)/(dx)f(x)=(1)/(3ln(x)) \cdot (d)/(dx)(3ln(x))` (1)

We also know that the derivative of the logarithm is

`(d)/(dx)ln(x)=(1)/(x)`

And since 3 is just a constant, expression (1) becomes:

`(d)/(dx)f(x)=(1)/(3ln(x)) \cdot (d)/(dx)(3ln(x))=(1)/(3ln(x))\cdot (3)/(x)=(1)/(xln(x))`

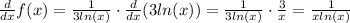
So, the derivative of the function is

`f'(x)=(1)/(xln(x))`