Question

Solve the inequality and express your answer in interval notation

Answer 1

`\begin{bmatrix}\mathrm{Solution:}\:&\:-6\le \:x<3\quad \mathrm{or}\quad \:x\ge \:5\:\\ \:\mathrm{Interval\:Notation:}&\:[-6,\:3)\cup \:[5,\:\infty \:)\end{bmatrix}`

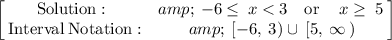
The number line graph is also attached below.

Explanation:

Given the inequality

`(\left(x-5\right)\left(x+6\right))/(\left(x-3\right))\ge 0`

`\:(x^2+x-30)/(\left(x-3\right))\ge \:0`

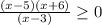
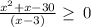
Let's find the critical points of the inequality.

`(x^2+x-30)/(\left(x-3\right))=0`

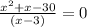
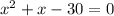`x^2+x-30=0` (Multiply both sides by x-3)

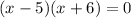`(x-5)(x+6)=0` (Factor left side of equation)

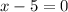`x-5=0` or
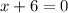`x+6=0` (Set factors equal to 0)

`x=5` or
`x=-6`

Check possible critical points.

x = 5 (Works in original equation)

x = −6 (Works in original equation)

Critical points:

x = 5 or x = −6 (Makes both sides equal)

x = 3 (Makes left denominator equal to 0)

Check intervals in between critical points. (Test values in the intervals to see if they work.)

x ≤ −6 (Doesn't work in original inequality)

−6 ≤ x < 3 (Works in original inequality)

3 < x ≤ 5 (Doesn't work in original inequality)

x ≥ 5 (Works in original inequality)

so

`-6\le \:x<3\quad \mathrm{or}\quad \:x\ge \:5`

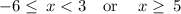
Therefore,

`\begin{bmatrix}\mathrm{Solution:}\:&\:-6\le \:x<3\quad \mathrm{or}\quad \:x\ge \:5\:\\ \:\mathrm{Interval\:Notation:}&\:[-6,\:3)\cup \:[5,\:\infty \:)\end{bmatrix}`

The number line graph is also attached below.