Question

Draw a rectangle that has a perimeter of 20 units and an area of 25 square units

Answer 1

Step-by-step explanation:

For any rectangle the dimensions are given by:

`w:width \\ \\ l:Length`

So the perimeter (P) is given by the following equation:

`P=2(w+l)`

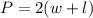
And the area is:

`A=w* l`

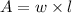
We know that:

`P=20units \\ \\ A=25units^2`

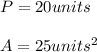
By substituting:

`20=2(w+l) \\ \\ \therefore w+l=10 \ \ldots eq1 \\ \\ \\ 25=w* l \ldots eq2`

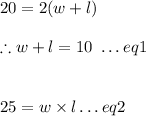
Solving for
`w` from eq1:

`w=10-l`

Substituting into eq2:

`25=(10-l)* l`

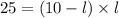
Then:

`\text{Solving for l:} \\ \\ \\ 10l-l^2=25 \\ \\ 10l-l^2-25=25-25 \\ \\ -l^2+10l-25=0 \\ \\ x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a) \\ \\ \\ a=-1,\:b=10,\:c=-25 \\ \\ \\ l_(1,\:2)=(-10\pm √(10^2-4\left(-1\right)\left(-25\right)))/(2\left(-1\right)) \\ \\ l_(1,\:2)=(-10\pm √(0))/(2\left(-1\right)) \\ \\ l=5`

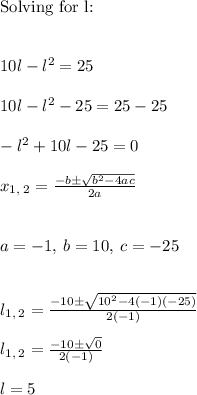
Solving for w:

`w=10-5=5`

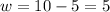
So this rectangle is a square and is shown below.