Question

A particle moves along the curve below. y = √ 8 + x 3 As it reaches the point ( 1 , 3 ) , the y -coordinate is increasing at a rate of 5 cm/s . How fast is the x -coordinate of the point changing at that instant? cm/s

Answer 1

The x-coordinate is changing at 10 cm/s

Explanation:

Rate of Change

Suppose two variables x and y are related by a given function y=f(x). If they both change with respect to a third variable (time, for instance), the rate of change of them is computed as the derivative using the chain rule:

`\displaystyle (dy)/(dt)=(dy)/(dx)\cdot (dx)/(dt)`

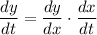
We have

`y=√(8+x^3)`

Or, equivalently

`y^2=8+x^3`

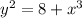
We need to know the rate of change of x respect to t. We'll use implicit differentiation:

`\displaystyle 2y\cdot (dy)/(dt)=3x^2\cdot (dx)/(dt)`

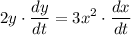
Solving for dx/dt

`\displaystyle (dx)/(dt)=(2y\cdot (dy)/(dt))/(3x^2)`

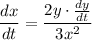
Plugging in the values x=1, y=3, dy/dt=5

`\displaystyle (dx)/(dt)=(2(3)\cdot 5)/(3\cdot 1^2)=10`

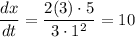
The x-coordinate is changing at 10 cm/s