Question

Working alone, Ryan can dig a 10 ft by 10 ft hole in five hours. Castel can dig the same while in six hours. How long would it take them if they worked together?

Answer 1

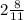`2(8)/(11)` hours.

Explanation:

Let t represent time taken in hours by both working together.

So part of work completed by working together in 1 hour would be
`(1)/(t)`.

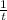We have been given that working alone, Ryan can dig a 10 ft by 10 ft hole in five hours. So part of work completed by Ryan in 1 hour would be
`(1)/(5)`.

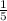We are also told that Castel can dig the same while in six hours. So part of work completed by Castel in 1 hour would be
`(1)/(6)`.

Since they will work together, so we can equate sum of work completed by both as:

`(1)/(t)=(1)/(6)+(1)/(5)`

`(1)/(t)* 30t=(1)/(6)* 30t+(1)/(5)* 30t`

`30=5t+6t`

`30=11t`

`11t=30`

`(11t)/(11)=(30)/(11)`

`t=2(8)/(11)`

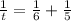
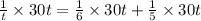
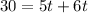
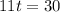
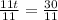
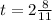
Therefore, it will take
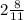`2(8)/(11)` hours to dig the pool working together.