To develop this problem we will apply the principle of dimensional similarity between water and air. Later we will leave the speed units defined in terms of the kinematic viscosity to finally contrast the magnitude of difference between them with the given values. Reynolds number can be defined as,
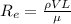
Here,
 = Density
= Density
V = Velocity of flow
L = length
 = Dynamic viscosity
= Dynamic viscosity
For dimensional similarity we have,
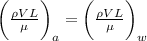
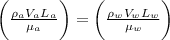
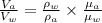
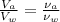
Here
 means the kinematic viscosity, then replacing with our values
means the kinematic viscosity, then replacing with our values

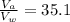
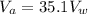
Therefore the velocity of air is higher than velocity of water by 35.1 times