Question

A plane can fly 475 miles against the wind in the same amount of time that it can fly 675 miles with the wind. If the wind speed is 40 mph, find the speed of the plane in still air.

Answer 1

230 mph

Explanation:

Let speed of plane in still air be x. Therefore, when against the wind speed, the resultant speed is x-40 mph. Equally, when with the wind speed, the resultant speed is x+40 mph. The time is the same hence we can express these as
`\frac {475}{x-40}=\frac {675}{x+40}`

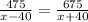
By cross multiplication

675(x-40)=475(x+40)

675x-27000=475x+19000

200x=46000

X=46000/200=230 mph